Java Hashtable with Example

Java Hashtable was part of java.util and it inherits dictionary class and implements the Map interface. Java Hashtable is similar to HashMap, but Hashtable is synchronized. Hashtable stores the key/values pair in a hash table.

How Hashtable works internally in java?

A Hashtable internally contains buckets in which it stores the key/value pairs. The Hashtable uses the key's hashcode to determine to which bucket the key/value pair should map. When you pass a key/value to the Hashtable, it queries the key's hashcode. The Hashtable uses that code to determine the bucket in which to place the key/value. So, for example, if the hashcode equals zero, the Hashtable places the value into Bucket 0. Likewise, if the hashcode is two, the Hashtable places the value into Bucket 2. (This is a simplistic example; the Hashtable will massage the hashcode first so the Hashtable doesn't try to insert the value outside the bucket.)
By using the hashcode this way, the Hashtable can also quickly determine in which bucket it has placed the value when you try to retrieve it. The hashcode only tells the Hashtable into which bucket to drop the key/value. Sometimes, however, multiple objects may map to the same bucket, an event known as a collision. In Java, the Hashtable responds to a collision by placing multiple values into the same bucket (other implementations may handle collisions differently).

Important points about Java Hashtable

1. Java Hashtable uses a hash table data structure.

2. Insertion order is not preserved and it is based on the hash code of keys.

3. Duplicates keys are not allowed but values may be duplicated.

4. Heterogeneous objects are allowed.

5. Java Hashtable doesn't allow null keys or null values.

6. It implements Serializable, Cloneable interface but not RandomAccessInterface.

7. Hashtable is thread-safe because every method defines in the Java Hashtable class is synchronized.

8. Java Hashtable is the best choice if our frequent operation is store and retrieves objects from a hash table.

Constructors in Java Hashtable:

Java Hashtable defines the following constructors.

1. Hashtable(): The first constructor is used to create a default hash table.

2. Hashtable(int size): This constructor is used to creates a hash table that has an initial size specified by size.

3. Hashtable(int size, float loadFactor): This constructor is used to creates a hash table that has an initial size specified by size and a load factor is specified by load factor.

4. Hashtable(Map m): This constructor is used to creates a hash table that is initialized with the elements in m.

Java Hashtable Methods: 

1. void clear(): This method is used to removes all key/values pair from a hash table and makes it empty.

2. Object clone(): It creates a shallow copy of this hash table.

3. boolean contains(Object value): This method returns true if some value equal to value exists within the hash table and returns false if the key is not found.

4. boolean containsKey(Object key): This method returns true if some key equal to key exists within the hash table else it returns false. 

5. boolean containsValue(Object value): It returns true if some value equal to value exists within the hash table else it returns false. 

6. Enumeration elements(): It returns an enumeration of the values contained in the hash table.

7. Object get(Object key): This method is used to remove the object that contains the value associated with a key and returned a null object if the key is not in the hash table.

8. boolean isEmpty(): It returns true if the hash table is empty else returns false.

9. Enumeration keys():  It returns an enumeration of the keys contained in the hash table.

10. Object put(Object key, Object value): This method is used to insert a key-value pair in the hash table.

11. void rehash(): This method is used to increases the size of the hash table and rehashes all of its keys.

12. Object remove(Object key): It removes a key and its value and returned a null object if the key is not in the hash table.

13. int size(): It returns the number of entries in the hash table.

14. String toString(): This method is used to returns the string equivalent of a hash table.

Reference: Java Hashtable Documentation

Java Hashtable Example:

 
import java.util.*;
class HashtableExample{
 public static void main(String args[]){
  
  //creating a hash table
  Hashtable<String, String> ht = new Hashtable<String, String>();
  
  Enumeration names;
  String key;
  
  //adding values in this hash table
  ht.put("Key 1", "Rahul");
  ht.put("Key 2", "Amit");
  ht.put("Key 3", "Vijay");
  ht.put("Key 4", "Suresh");
  ht.put("Key 5", "Prashant");
  
  //returns size of the hash table
  System.out.println("Hash table size is: "+ht.size());
  
  //checks hash table is empty or not
  System.out.println("Hash table is empty or not: "+ht.isEmpty());
  
  //returns true if hash table contains specified value 
  System.out.println("Hash table contains specified value or not: "+ht.containsValue("Prashant"));
  
  names = ht.keys();
  while(names.hasMoreElements()){
   key = (String)names.nextElement();
   System.out.println("Key is: " +key + " & its Value is: " +ht.get(key));
  }
  
  ht.clear();
  System.out.println("Removes all the key-value pair: "+ht);
 }
}

Output:

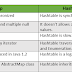
Hashtable vs HashMap:

Hashtable and HashMap both are part of the java.util and both are used to store data in the form of key-value pairs. Both are using hashing techniques to store unique keys. But there are many differences between Hashtable and HashMap which is very important for you to know the Java interview point of view. Let's see the differences between Hashtable and HashMap.

1. Hashtable is synchronized while the HashMap is not synchronized.
2. Hashtable doesn't allow you to store null key and null value on the other hand HashMap allow you to store one null key and multiple null values.
3. HashMap is fast while Hashtable is slow due to synchronization.
4. HashMap is traversed by Iterator while Hashtable is traversed by both Enumeration and Iterator.
5. HashMap was introduced in Java 1.2 while Hashtable is a legacy class.
6. HashMap inherits the AbstractMap class on the other hand Hashtable inherits the dictionary class.

Comparison table:

You may also enjoy these related posts:
1. How to use TreeMap in Java with Example?
2. How to add and remove elements from ArrayDeque?
3. Comparable vs Comparator interface in Java with Example
4. Java TreeSet with Example
5. How to implement a stack data structure in Java?
6. How to implement a LinkedList in Java?
7. How to add or remove elements from ArrayList?